python实现神经网络

1.使用sklearn datasets产生数据集

Sklrarn简介

• Scikit-learn(sklearn)是基于Python语言的机器学习工具，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。他是简单高效的数据挖掘和数据分析工具，可供大家在各种环境中反复使用。

sklearn的安装

• Sklearn安装要求Python(>=2.7 or >=3.3)、NumPy (>= 1.8.2)、SciPy (>= 0.13.3)。如果已经安装NumPy和SciPy，安装scikit-learn可以使用pip install -U scikit-learn进行安装。

使用datasets产生数据集

import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
def generate_data():
	np.random.seed(0)
	X, y = datasets.make_moons(200, noise=0.20)
	plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
	plt.show()
    return X,y
def main():
    X, y = generate_data()
if __name__ == "__main__":
    main()

• make_moons(n_samples=100, shuffle=True, noise=None, random_state=None):

  n_numbers:生成样本数量
  shuffle:是否打乱，类似于将数据集random一下
  noise:默认是false，数据集是否加入高斯噪声
  random_state:生成随机种子，给定一个int型数据，能够保证每次生成数据相同。

这里就是生成月牙形的200个样本，加入了高斯噪声。

• plt.scatter(X,Y,c = 'b',marker = 'o',cmap = None,norm = None,vmin = None.vmax = None,alpha = None,linewidths = None,verts = None,hold = None,**kwargs)

  X和Y是长度相同的序列，c是色彩颜色的序列，marker是色彩形状的参数；cmap:colormap颜色映射；norm:数据亮度0-1；vmin,vmax:亮度设置；

  cmap = plt.cm.Spectral实现的功能是给label为1的点一种颜色，给label为0的点另一种颜色。

  X[:,0]取矩阵X中0列的全部元素；X[:,1]取矩阵X中1列的全部元素

  s:散点的大小参数；np.squeeze()去除单位条目

• 以下就是生成的数据集分布图：

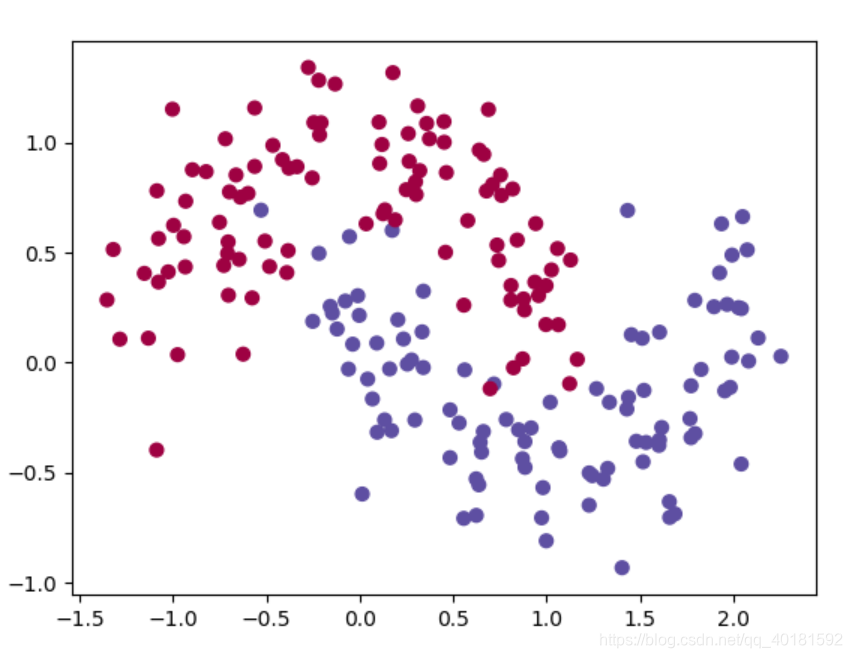
2.使用Logistic回归进行分类

• 为了对比神经网络和Logistic回归的差别，下面先采用逻辑回归进行分类，采用sklearn中Logistic Regression类，当然也可以使用之前所讨论的代码，这里为了方便直接进行方法调用。

  def classify(X, y):
  	"""Logistic 分类"""
      clf = linear_model.LogisticRegressionCV()  # 生成Logistic分类器
      clf.fit(X, y) # 对产生的数据进行分类
      return clf
  
  def plot_decision_boundary(pred_func, X, y):
  	"""画决策边界线"""
      # 设置图像边界最大值与最小值
      x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
      y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
      h = 0.01 #采样间隔
      # 生成网格矩阵
      xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
      # 对整个网格矩阵进行预测
      Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
      Z = Z.reshape(xx.shape) # 使预测结果重新变成网格数组大小
      # 画出决策边界
      plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
      # 画出数据点
      plt.scatter(X[:, 0], X[:, 1], s = 20,c=y, cmap=plt.cm.Spectral)
      plt.show()
  
  def main():
      X, y = generate_data()
      clf = classify(X, y)
      plt.title("Logistic Regression")
      plot_decision_boundary(lambda x: clf.predict(x),X,y)
  if __name__ == "__main__":
      main()

• X,Y = numpy.meshgrid(x, y)#生成网格矩阵
  输入的x，y，就是网格点的横纵坐标列向量（非矩阵）
  输出的X，Y，就是坐标矩阵

• Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

  因为前面产生的网格矩阵是多维数组，ravel函数将多维数组降为一维，仍返回array数组，元素以列排列。之后调用np.c_[]将xx.ravel()得到的列后增加一列yy.ravel()。

  numpy.c_[] 和np.r_[]可视为兄弟函数，两者的功能为np.r_[]添加行，np.c_[]添加列。

• Z = Z.reshape(xx.shape)

  将网格坐标预测的结果转化成与网格坐标一致规格的数组，使其一一对应，xx代表横坐标，yy代表纵坐标，Z代表网格坐标预测的结果。

• plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)

  由于contourf可以填充等高线之间的空隙颜色，呈现出区域的分划状，所以很多分类机器学习模型的可视化常会借助其展现。

  下面是用Logistic回归生成的决策边界，可以发现他仅仅是从中间划开，边界线是一条直线，分类效果不好。

3.搭建一个三层的神经网络

• 根据前面神经网络的讨论，下面我们搭建一个简单的三层的神经网络，包含一个输入层，一个隐藏层和一个输出层。输出层的节点为数据的维度，这里为2，（因为这里的分类只有0/1，如果有多个类别的话，维度就不是2了），神经网络的输入为x，y的坐标，整个框架为下图所示：

  

​ 对于隐藏层的维度可以自己选择，如果节点过多，则意味着计算更复杂，所付出的成本也更多，也容易造成过拟合从而影响判断，具体的节点数取值稍后会对比分析，观察节点数的不同对神经网络的输出有什么影响。

​ 之前在讨论神经网络的时候说到，每一层的输出到下一层都需要一个激活函数，前面讨论的是sigmoid函数，其实还有tanh函数等，在这里为了求导方便我们采用的是tanh激活函数，后面可以根据需要将激活函数修改为sigmoid函数对比分析效果。

前向传播（正向传播）

• 前向传播就是指一组矩阵的相乘以及我们之前提到的激活函数。假设x是对神经网络的二维输入，那么我们按照如下步骤计算我们的预测结果：

  $$z_1 = X *\theta_1 + b_1 \\a_1 = tanh(z_1) \\z_2 = a_1* \theta_2+b_2\\a_2 = y' =softmax(z_2)\\ z_i代表第i层的输入；a_i代表第i层用激活函数后的输出；\\ \theta 和b是神经网络的参数矩阵，后面通过学习来获得最佳值$$

损失函数（评价函数）

• 为神经网络学习到最佳的参数，以此达到使错误最小的目标，我们必须要定义一个损失函数来衡量错误，对于softmax()函数输出来说，我们通常使用的是分类交叉熵损失（categorical cross-entropy loss，又称为负对数似然 negative log likelihood）

• softmax()函数是将神经网络输出的值转化为0-1之间的概率，从而可以很好得判断分类的结果。他的公式如下所示：

  $$p_i = \frac{e^{a_i}}{\sum_{k=1}^{N}e_k^a}$$

  p为最后输出的概率分布；N为输入的训练数据个数；a为用激活函数后的输出；

  ———————该函数的推导过程在文章末尾的链接中，在此不再赘述。———————

  #python中softmax函数的实现：
  def softmax(X):
  	exps = np.exp(X)
  	return exps / np.sum(exps)

• 交叉损失熵函数是softmax的好兄弟，一般用他来评价损失，他的公式如下：

  $$L(y,y')=-\frac{1}{N}\sum_{n\epsilon N}\sum_{i\epsilon C}y_{n,i}logy'_{n,i}$$

  N为训练数据个数；C为输出的类别；y’是输出的概率结果；y为实际的结果

  ——————-注意不同的激活函数他的交叉损失熵函数是不一样的，该推导过程以及其他激活函数的交叉损失熵函数在文章末尾的链接给出，在此不再赘述。————————-

  def cross_entropy(X,y):
      m = y.shape[0]
      p = softmax(X)
      log_likeihood = -np.log(p[range(m),y])
      loss = np.sum(log_likeihood) / m
      return loss

反向传播（梯度下降）

• 前面的文章中我们以及讨论了用梯度下降法来寻找损失函数的最小值。我会用固定的学习率实现一个最普通版本的梯度下降法，也称为批量梯度下降法，它的变化版本比如随机梯度下降法和小批量梯度下降法在实践中通常表现得更好。

​ 根据上一篇文章所述，反向传播的推导过程也不再赘述，这里就给出所需要的公式计算：

$$\delta_3 = y' -y\\ \delta_2=(1-tanh^2z_1)*\delta_3 \\ \frac{\partial L}{\partial \theta_2} = a_1^T\delta_3 \\ \frac{\partial L}{\partial b_2} = \delta_3 \\ \frac{\partial L}{\partial \theta_1} = X^T\delta_2 \\ \frac{\partial L}{\partial b_1} = \delta_2$$

4.代码实现

# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt 
import numpy as np 
from sklearn import datasets
import matplotlib 

def generate_data(): # 产生数据集
    np.random.seed(0)
    X, y = datasets.make_moons(200, noise=0.20) # 产生月牙形状的数据集
    return X, y

def plot_decision_boundary(pred_func, X, y): # 画决策边界线
    # 设置图像边界最大值与最小值
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01 #采样间隔
    # 生成网格矩阵
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 对整个网格矩阵进行预测
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape) # 使预测结果重新变成网格数组大小
    # 画出决策边界
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    # 画出数据点
    plt.scatter(X[:, 0], X[:, 1], s = 20,c=y, cmap=plt.cm.Spectral) 

def calculate_loss(X, y, param, reg_lambda, num_examples): # 计算损失
    #获得参数
    theta1, b1, theta2, b2 = param['theta1'], param['b1'], param['theta2'], param['b2'] 
    #前向传播
    z1 = X.dot(theta1) + b1 
    a1 = np.tanh(z1) 
    z2 = a1.dot(theta2) + b2 
    exp_scores = np.exp(z2) 
    
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) 
    # 计算损失
    corect_logprobs = -np.log(probs[range(num_examples), y]) 
    data_loss = np.sum(corect_logprobs) 
    # 正则化（防止过拟合）
    data_loss += reg_lambda/2 * (np.sum(np.square(theta1)) + np.sum(np.square(theta2))) 
    return 1./num_examples * data_loss 

def predict(param, x): # 预测结果
    theta1, b1, theta2, b2 = param['theta1'], param['b1'], param['theta2'], param['b2'] 
    # 前向传播 
    z1 = x.dot(theta1) + b1 
    a1 = np.tanh(z1) 
    z2 = a1.dot(theta2) + b2 
    exp_scores = np.exp(z2) 
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) #按行相加，保证矩阵的二维特性
    return np.argmax(probs, axis=1) #表示返回行上最大值得索引值
 
def build_model(X, y, nn_input_dim, nn_hdim, nn_output_dim, alpha, reg_lambda, num_passes=20000, print_loss=False): # 模型建立
    # - nn_input_dim: 输入层维度
    # - nn_hdim: 隐藏层维度
    # - nn_output_dim: 输出层维度
    # - alpha: 学习速率
    # - reg_lambda: 正则化参数lanmda
    # - num_passes: 学习代数
    # - print_loss: 是否打印每一代的损失
    num_examples = len(X) # 数据集个数
    # 初始化参数
    np.random.seed(0) 
    theta1 = np.random.randn(nn_input_dim, nn_hdim) / np.sqrt(nn_input_dim) 
    b1 = np.zeros((1, nn_hdim)) 
    theta2 = np.random.randn(nn_hdim, nn_output_dim) / np.sqrt(nn_hdim) 
    b2 = np.zeros((1, nn_output_dim)) 
    # 参数字典
    param = {} 
    loss_list = []
    # 梯度下降 
    for i in range(0, num_passes): 
        # 前向传播 
        z1 = X.dot(theta1) + b1 
        a1 = np.tanh(z1) 
        z2 = a1.dot(theta2) + b2 
        exp_scores = np.exp(z2) 
        probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) 
        # 反向传播 
        delta3 = probs 
        delta3[range(num_examples), y] -= 1 
        dtheta2 = (a1.T).dot(delta3) 
        db2 = np.sum(delta3, axis=0, keepdims=True) 
        delta2 = delta3.dot(theta2.T) * (1 - np.power(a1, 2)) 
        dtheta1 = np.dot(X.T, delta2) 
        db1 = np.sum(delta2, axis=0) 
        # 加入正则化
        dtheta2 += reg_lambda * theta2 
        dtheta1 += reg_lambda * theta1 
        # 梯度下降参数更新
        theta1 += -alpha * dtheta1 
        b1 += -alpha * db1 
        theta2 += -alpha * dtheta2 
        b2 += -alpha * db2  
        param = { 'theta1': theta1, 'b1': b1, 'theta2': theta2, 'b2': b2} 
        # 每隔1000代打印损失
        #loss_list.append(calculate_loss(X,y,param,reg_lambda,num_examples))
        if print_loss and i % 1000 == 0: 
            print("Loss after iteration %i: %f" %(i, calculate_loss(X,y,param,reg_lambda,num_examples))) 
            
    return param,loss_list
def main():
    X, y = generate_data()
    nn_input_dim = 2 # 输入层维度 
    nn_output_dim = 2 # 输出层维度
    alpha = 0.01 # 梯度下降学习速率 
    reg_lambda = 0.01 # 正则化参数
    param, loss_list = build_model(X, y, 2, 3, 2, alpha, reg_lambda, print_loss=True)
    # 画出决策边界
    plot_decision_boundary(lambda x: predict(param, x),X,y) 
    plt.title("Decision Boundary for hidden layer size 3") 
    #plt.figure(3)
    #plt.plot(range(0,len(loss_list)),loss_list)
    # 改变隐藏层维度
    plt.figure(2)
    hidden_layer_dimensions = [1, 2, 3, 4, 5, 20, 50] 
    for i, nn_hdim in enumerate(hidden_layer_dimensions):  
        plt.subplot(4, 2, i+1) 
        plt.title('Hidden Layer size %d' % nn_hdim) 
        param, loss_list = build_model(X,y,2,nn_hdim,2,alpha,reg_lambda) 
        plot_decision_boundary(lambda x: predict(param, x),X,y)
    plt.show()
if __name__ == '__main__':
    main()

• 可以发现当隐藏层维度为3时，分类效果较好，对比之前的Logistic回归有更好的突破，下面是通过改变隐藏层的大小观察对输出结果的影响：

• 可以发现低维度的隐藏层可以更好得捕获决策边界，而高维度得隐藏层则更容易出现过拟合，另一方面我们已经加入了正则化目的就是要消除过拟合，结果仍然可以看到维度过高虽然可以非常精确得描述分类效果，但是不是一般情况，故隐藏层的维度选择是一个重要的方面，其次可以改变学习速率和正则化强度来观察对输出结果的影响。

• 可以改进的方面：

  增加隐藏层，观察对输出结果的影响。

  改变输入数据的类别，增加到3类等等。

  改变激活函数，本文使用的是tanh双曲正切函数，可以改成sigmoid函数，推导反向传播公式（上一篇已经推导）观察不同的激活函数对输出结果的影响。

5.结尾（附录）

• 本次主要讨论了python实现一个简单的神经网络，目的在于熟悉神经网络的内部工作过程，便于更好的理解神经网路的工作原理，这里的计算过程并不是高效的，但是非常容易理解，后面会通过Tensorflow更方便地搭建神经网络。
• 本篇文章参考于http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/
• 代码是经过自己修改之后的，原项目的github链接为：https://github.com/dennybritz/nn-from-scratch
• softmax和交叉熵的深度解析和python实现：https://blog.csdn.net/Gipsy_Danger/article/details/81292148
• 交叉熵损失函数的推导：https://blog.csdn.net/red_stone1/article/details/80735068

---

​ 作者也是初学机器学习，上述仅为自己的理解，难免有不正确的地方，请读者及时指正，共同进步。