说在前面
- 本文参考了 https://blog.csdn.net/jiaoyangwm/article/details/79525237这篇博客,这篇博客写的很好,值得推荐,就是里面有一个错误是列表拷贝的问题,要用到深拷贝。否则会使属性列表清空计算的信息增益为0。
- 其次参考了西瓜书中的叙述,这里决策树的信息增益其实和信息论相联系。
- 本篇文章是从jupyter notebook 中直接导出的,后面添加了图片,格式稍微有点不美观。
1.决策树(decision tree)
- 是一种基本的分类与回归方法,此处主要讨论分类的决策树。在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
- 决策树通常有三个步骤:特征选择、决策树的生成、决策树的修剪。
- 用决策树分类:从根节点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子节点,此时每个子节点对应着该特征的一个取值,如此递归的对实例进行测试并分配,直到到达叶节点,最后将实例分到叶节点的类中。
2.决策树的构建
- 决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分,也对应着决策树的构建。
(1) 开始:构建根节点,将所有训练数据都放在根节点,选择一个最优特征,按着这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下最好的分类。
(2) 如果这些子集已经能够被基本正确分类,那么构建叶节点,并将这些子集分到所对应的叶节点去。
(3)如果还有子集不能够被正确的分类,那么就对这些子集选择新的最优特征,继续对其进行分割,构建相应的节点,如果递归进行,直至所有训练数据子集被基本正确的分类,或者没有合适的特征为止。
(4)每个子集都被分到叶节点上,即都有了明确的类,这样就生成了一颗决策树。
信息增益
- 划分数据集的大原则是:将无序数据变得更加有序,但是各种方法都有各自的优缺点,信息论是量化处理信息的分支科学,在划分数据集前后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择,所以必须先学习如何计算信息增益,集合信息的度量方式称为香农熵,或者简称熵。
熵定义为信息的期望值,如果待分类的事物可能划分在多个类之中,则符号$x_i$的信息定义为:
为了计算熵,我们需要计算所有类别所有可能值所包含的信息期望值,通过下式得到:
其中,n为分类数目,熵越大,随机变量的不确定性就越大。
当熵中的概率由数据估计(特别是最大似然估计)得到时,所对应的熵称为经验熵(empirical entropy)。什么叫由数据估计?比如有10个数据,一共有两个类别,A类和B类。其中有7个数据属于A类,则该A类的概率即为十分之七。其中有3个数据属于B类,则该B类的概率即为十分之三。浅显的解释就是,这概率是我们根据数据数出来的。我们定义样本数据表中的数据为训练数据集D,则训练数据集D的经验熵为H(D),|D|表示其样本容量,及样本个数。设有K个类Ck,k = 1,2,3,···,K,|Ck|为属于类Ck的样本个数,这经验熵公式可以写为:
在理解信息增益之前,要明确——条件熵
信息增益表示得知特征X的信息而使得类Y的信息不确定性减少的程度。
条件熵H(Y∣X)H(Y∣X)表示在已知随机变量X的条件下随机变量Y的不确定性,随机变量X给定的条件下随机变量Y的条件熵(conditional entropy) H(Y|X),定义X给定条件下Y的条件概率分布的熵对X的数学期望:信息增益:信息增益是相对于特征而言的。所以,特征A对训练数据集D的信息增益Gain(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:
一般地,熵H(D)与条件熵H(D|A)之差成为互信息(mutual information)。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
信息增益比(增益率):特征A对训练数据集D的信息增益比Gain_ratio定义为其信息增益Gain(D,A)与训练数据集D的经验熵之比:
3.计算经验熵(信息熵)

1 | from math import log |
1 | def calculate_Ent(dataSet): |
1 | {'是': 8, '否': 9} |
1 | 0.9975025463691153 |
4.计算信息增益
1 | def split_dataSet(dataSet,axis,value): |
1 | {'是': 8, '否': 9} |
5.用ID3算法构建决策树
- ID3算法的核心是在决策树各个结点上对应信息增益准则选择特征,递归地构建决策树。
具体方法是:
(1)从根结点(root node)开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征。
(2)由该特征的不同取值建立子节点,再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止;
(3)最后得到一个决策树。
1 | import operator |
1 | {'是': 8, '否': 9} |
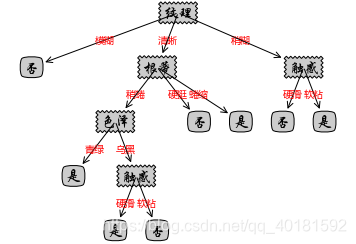
6.绘制决策树
1 | import pandas as pd |